Linear Algebra

Vector

1. Geometric vectors
   우리가 흔히 중고등학교때 배운 vector의 개념
2. Polynomials
   다항식 또한 vectors이다. 두 다항식은 더할수있고 scalar배또한 할 수 있다.
   따라서 Polynomials are Instance of Vecors
3. Elements of $\Bbb{R}^n$
   $a,b\in\Bbb{R}^3$ 일때 $a+b = c \in\Bbb{R}^3$
   스칼라로 곱해도 속한다

Linear algebra는 이러한 비슷함에 초점을 둔다.

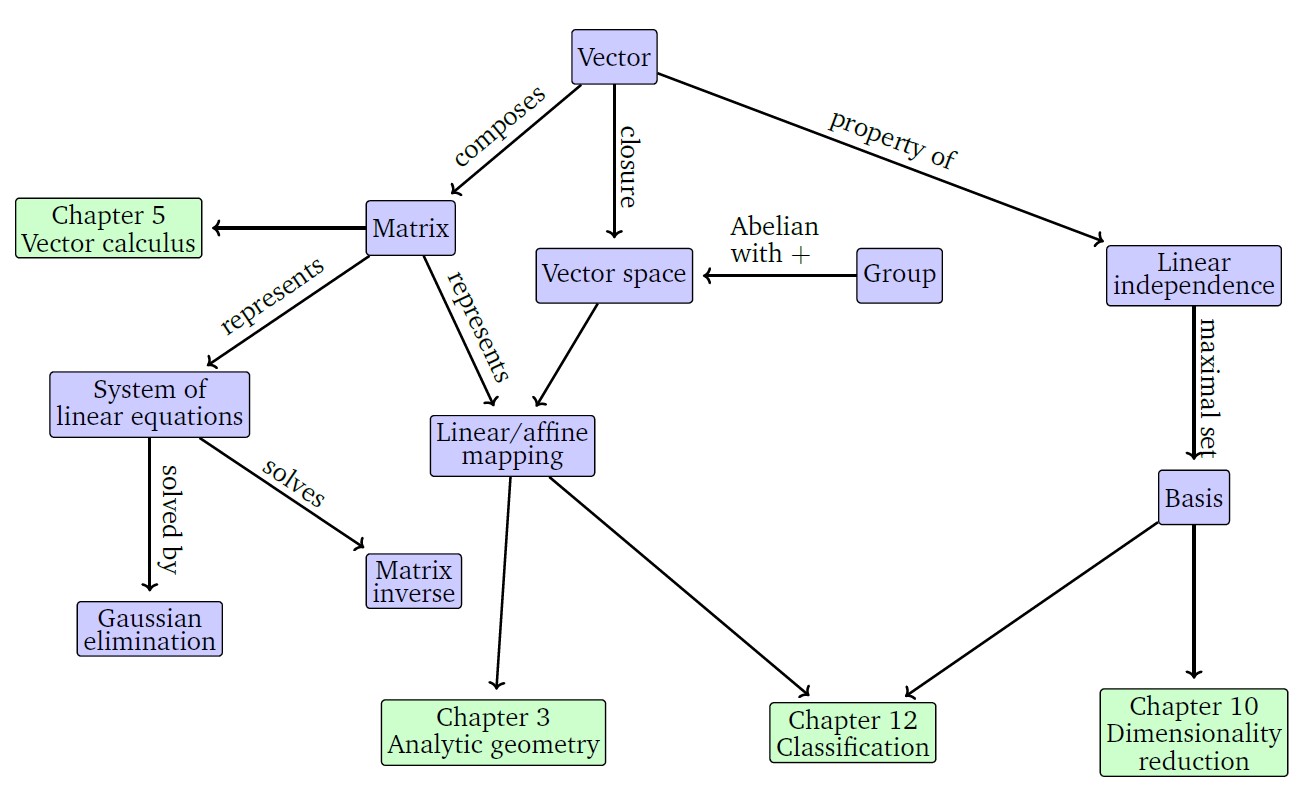{: .align-center}

Vector space의 개념과 성질이 매우 ML에서 매우 중요하다.
Vector space란 작은 Vector의 집합들끼리 서로 더하고 Scailing하여서 나온 집합이다.

2.1 Systems of linear equations

Example 2.1

{: .align-center}
Product N_n을 위해 Resource R_m 이 필요한경우

• 제한량 : b_j
• Product i 생산을 위해 필요한 Resource R_j의 양: a_ij
• Product i 의 생산량 : x_i

위와 같은 선형 방정식을 간단하게 만들기 위해 matrix를 사용

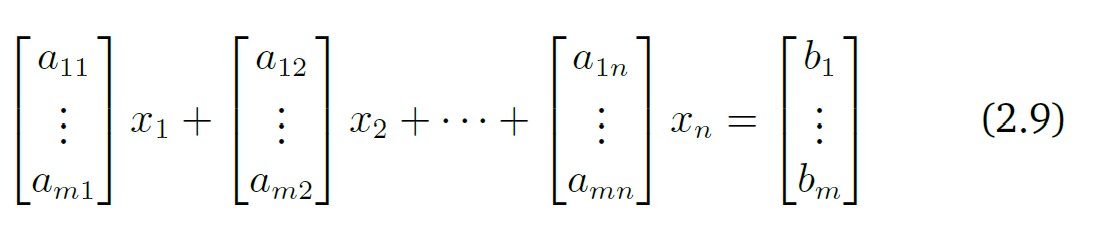{: .align-center}{: width=”50%” height=”50%”}

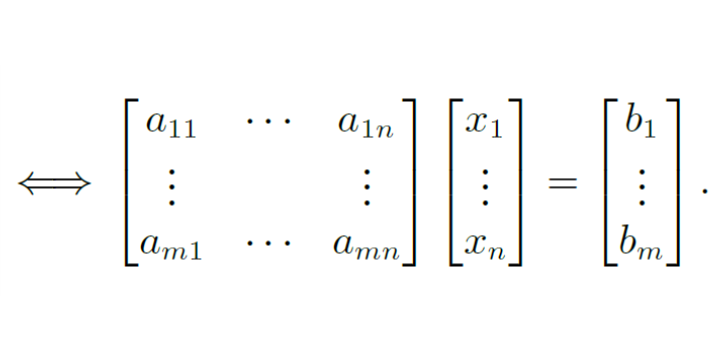{: .align-center}{: width=”50%” height=”50%”}

2.2 Matrix

행렬의 기본법칙은 이미 선형대수학 시간에 학습하였으니 넘어가겠다.

2.3 Solving Systems of Linear Equation

2.3.1 Particular and General Solution

해를 구하는 방법을 알기에 앞서 Linear Equation의 해에대하여 알아보자.

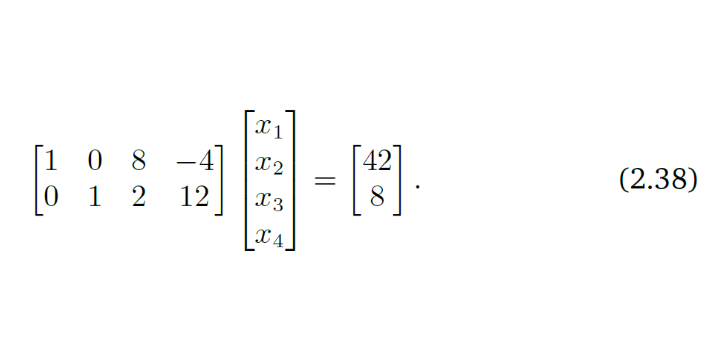
위의 행렬식을 보면 2개의 방정식과 4개의 미지수가 있다. 따라서 무수히 많은 근이 존재할 것이다.

Ax = b 라는 compact한 식으로 나타낸뒤 해를 첫번째 column C1의 42 두번째 column C2의 8배로 나타낼 수 있다

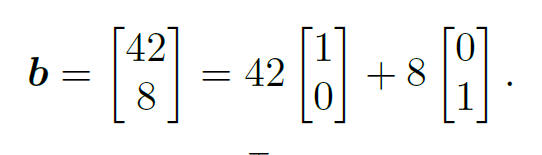
따라서 이의 해는 $[42,8,0,0]^T$ 로 나타낼수 있다. 이러한 식은 무수히 많은 해중 단 하나의 해이기 때문에 이를==Particular solution==이라고 부른다.

이제 모든 해를 일반적으로 표현하기 위하여 수학적 techinque을 사용한다. 0을 더함으로서 양변의 equality는 보존됨으로, 0을 만들어 내보자.

세번째 column을 1,2번째 column의 합으로 표현해 보면

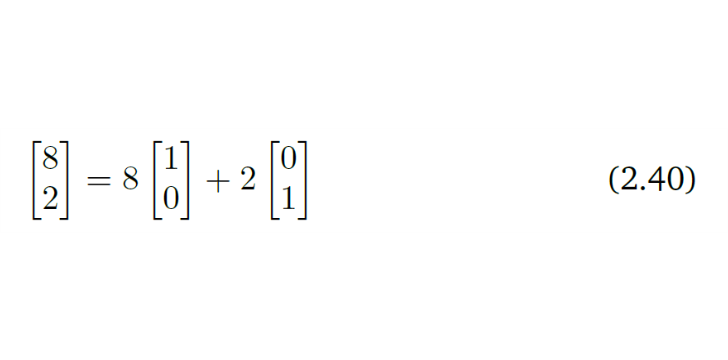
따라서 0 = 8C1+ 2C2- 1C3 +0C4 로 나타낼수 있고 이들의 계수인 [8,2,-1,0]^T^ 가 바로 0을 만들어 내는 Vector이다.

또한 이 해(Vector)의 scalar배수들 또한 같은 결과를 가진다.

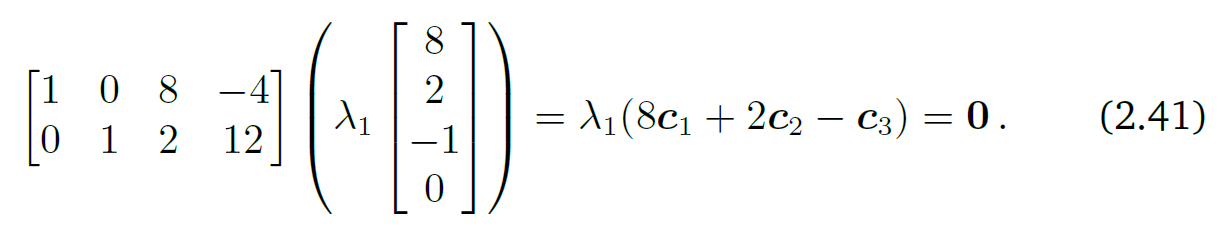
따라서 이후 작성…..

출처 : Marc Peter Deisenroth, Mathmatics for Machine Learning,(Cambridge University Press)