Numpy & Basic Math1

Start

Numpy

큰 matrix를 파이썬으로 표현하기 위해 사용

• 그리고 memory를 효율적으로 사용하기 위해

• 반복문 없이 데이터 배열처리를 지원함

ndarray

import numpy as np

test_array = np.array([1,2,3,4],float)

ndarry 와 list 의 차이점

• numpy는 하나의 데이터 type만 배열에 들어갈수 있다
• dynamic typing이 안됨

numpy는 차례대로 데이터가 바로 메모리에 할당되지만

python의 list는 주소값을 메모리에 저장하게 되어 2번을 거쳐서 값을 불러옴

따라서 값이 ndarray의 값이 같더라도 is 를 써보면 false가 나온다

list는 아님

array의 rank

rank 0 : scalar

rank 1 : vector

rank 2 : matrix

rank 3 : 3- tensor

rank 4 : n-tensor

dtype : numpy는

nbytes

ndarray의 object 메모리 크기를 반환함

Shape

reshape

Array의 shape 크기를 변경함, element의 갯수는 동일

import numpy as np
test_matrix = [[1,2,3,4],[1,2,3,4]]
np.array(test_metrix).reshape(2,4)
np.array(test_metrix).reshape(-1,2).shape
# (4,2)

flatten

다차원 array를 1차원 array로 변환

Indexing

리스트와 달리 [0,0]과 같은 접근법을 허용한다

Slicing

data를 접근 할 때 slicing을 굉장히 많이 쓴다

이건 많이 써봐서 ㄱㅊ

#건너 뛰는것도 씀
arr[:,::2]
#2칸씩 건너 뛰는

Creation Function

np.arange(0, 10, 0.5)
#array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. ,6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])

np.zeros(shape = (10,),dtype =np.int8)
np.empty(shape = (10,),dtype =np.int8)
#empty함수는 memory에 빈공간이 잡힘 그안에는 쓰레기 값이 있음

identity

단위행렬 (i행렬)을 생성함

eye

대각선이 1인행렬, k값의 시작 index 지정가능

diag

대각행렬 값을 추출함

random sampling

데이터 분포에 따른 sampling으로 array를 생성

• np.random

Operation function

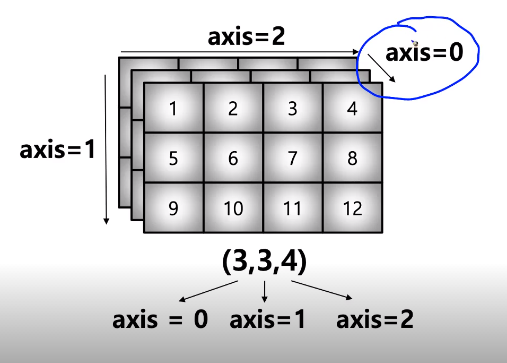
Axis

기준이되는 dimension 축

test_array = np.arrange(1,13).reshape(3,4)
'''
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
'''
test_array.sum(axis=1)
#(array([10,26,42]))

Concatenate

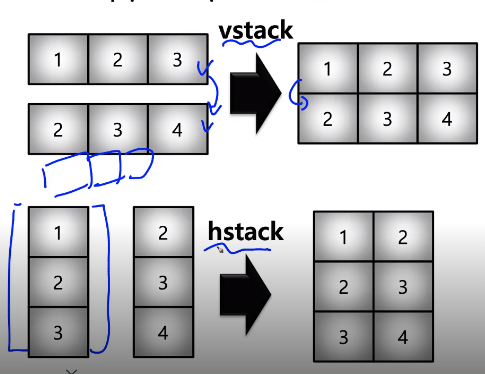
• numpy array를 붙이는 함수
• np.concatenate((a,b),axis = 0)
• 값을 붙일때 2개 함수 concatenate,hstack,vstack
• 맞춰서 축을 늘리고 싶은때 newaxis 사용

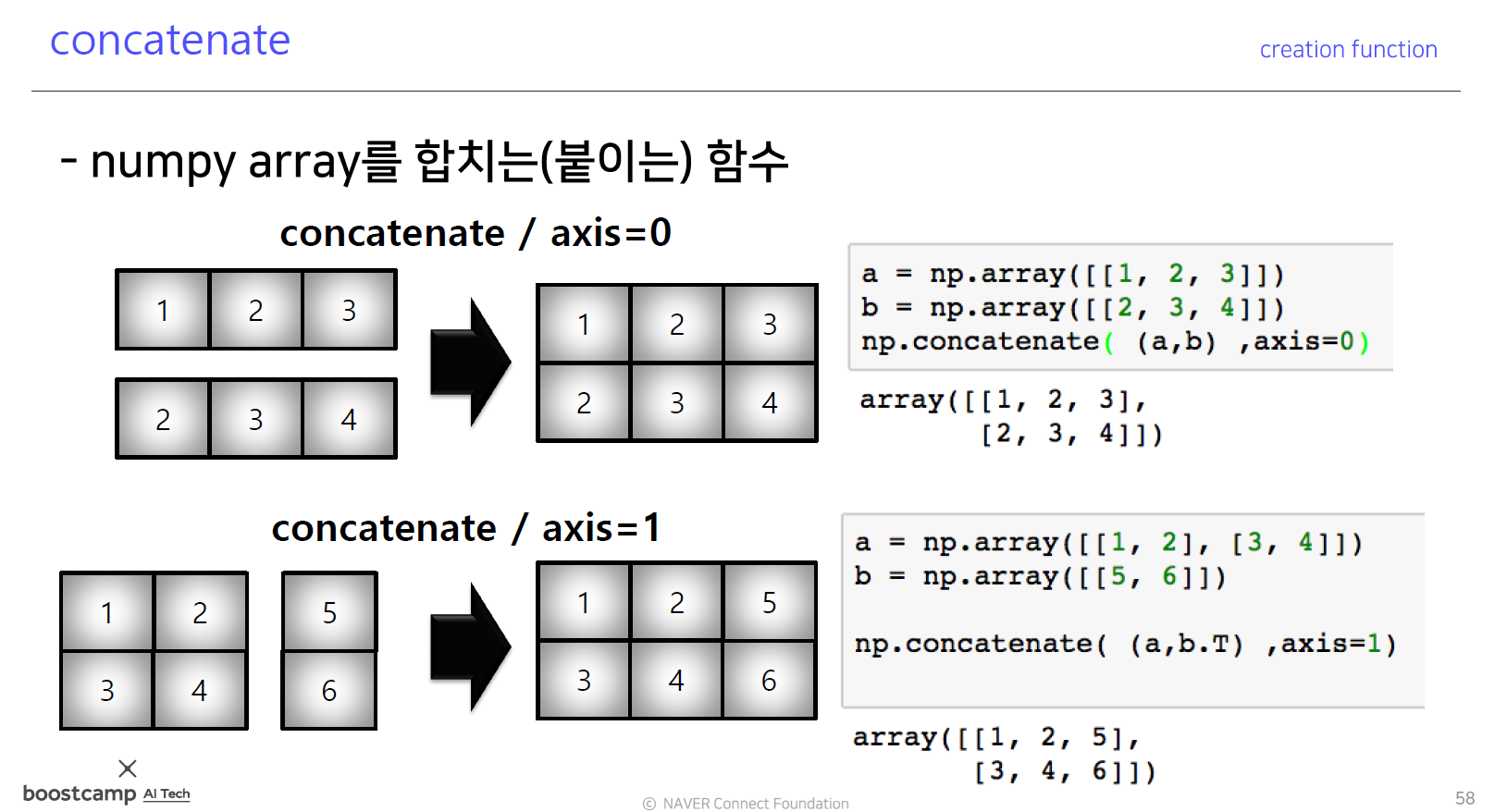
이게 생각보다 익숙하지 않아서 연습이 좀 필요할듯 싶다

행렬의 dot product

• a.dot(test_b)

Transpose

• test_a.T

Broadcasting

(element wise operation : array의 shape이 같아서 각각 연산)

Broadcasting은 크기가 shape이 다를때 알아서 퍼져서 연산이 일어남

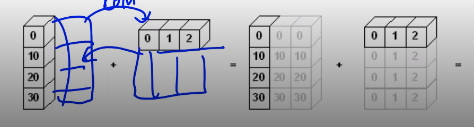
요런느낌

test_matrix = np.arange(1, 13).reshape(4, 3)
test_vector = np.arange(10, 40, 10)
array([10, 20, 30])

test_vector.reshape(-1, 3).T + test_vector
'''
array([[20, 30, 40],
       [30, 40, 50],
       [40, 50, 60]])
'''
# 이런 계산도 가능함

Numpy performance

• 연산의 속도는 list보다 훨씬 크다 (dynamic typing을 포기한 결과)
• 하지만 할당에서는 연산속도의 이점이 없음

Comparison

import numpy as np

a = np.arrange(10)
a<4
'''
array([ True,  True,  True,  True, False, False, False, False, False,
       False])
'''
np.any(a>5)
# 하나라도 true면 전체가 True다
np.all(a>5)
#하나라도 false면 전체가 false이다

#numpy 배열간의 shape이 동일할때는 element간의 크기를 비교

np.logical_and(a>0,a<3)
#조건의 and
np.logical_not(b)
np.logical_or(a>0,a<3)

# np.where
np.where(a > 5)
#(array([6, 7, 8, 9], dtype=int64),
np.where(a>5,3,2)
# array([2, 2, 2, 2, 2, 2, 3, 3, 3, 3])


# argmax : 가장 큰값의 index 반환, argmin : 가장 작은값의 index반환
a = np.array([1,2,3],[4,5,6],[7,8,9])
a.argmax(axis = 0)

Boolean Index

index에 조건을 넣어주어 조건을 만족하는 해당하는 값만 뽑아옴

import numpy as np

a = np.arange(10)
condition = a>5
a[condition]
# array([6, 7, 8, 9])

Fancy index

index값을 넣어줌

a = np.array([2, 4, 6, 8], float)
cond1 = np.array([1, 1, 1, 2, 1, 1, 1, 3])
cond2 = np.array([1, 1, 1, 2, 1, 1, 1, 2])
a.take(cond1)
#array([4., 4., 4., 6., 4., 4., 4., 8.])
a[cond]
#array([4., 4., 4., 6., 4., 4., 4., 8.])
#다차원 리스트에 적용
a = np.array([[1,2,3,4],[3,4,2,2],[0,0,0,0],[1,1,2,1]])
a[cond1,cond2]
#array([4, 4, 4, 0, 4, 4, 4, 2])

Vector

What is vector

• 벡터는 숫자를 원소로 가지는 리스트 또는 배열
• 공간에서 한점을 나타낸다 (원점으로 부터 상대적 위치)

Hadamard product (element product)

성분곱이란 같은 shape에서의 각 element끼리의 곱

Vector의 덧셈 & 뺄셈

원점으로 부터가 아닌 다른 벡터로 부터 상대적 위치이동

뺄셈은 방향을 뒤집은 덧셈

벡터의 norm

• 어떠한 벡터의 원점에서부터의 거리
• 기호 밑 표현

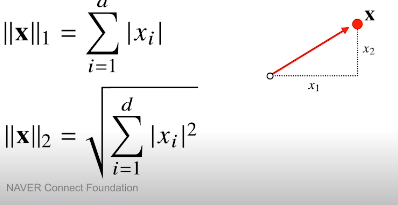
norm은 임의의 차원 d에서 성립

L1 norm

각성분의 변화량의 절대값

좌표명면에서 각좌표축을 따라 이동하는 거리의 합 :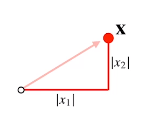

L2 norm

**피타고라스 정리를 이용해 유클리드 거리를 계산 ** :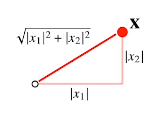

왜 다른 norm을 사용하나?

• norm의 종류에 따라 기하학적 성질들이 달라진다
• 

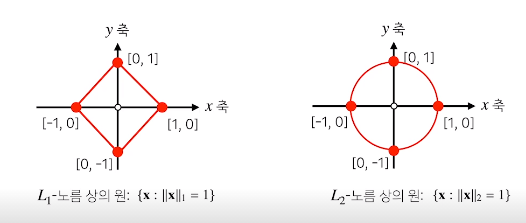
원의 정의 : 원점에서 부터 거리가 r 인 점들의 집합

norm을 사용하여 두벡터 사이의 거리를 구하자

L1 norm을 사용하여 구한 벡터사이의 거리

L2 norm을 사용하여 구한 벡터사이의 각도

행렬

행렬이란 행벡터를 원소로 가지는 이차원 배열

전치행렬

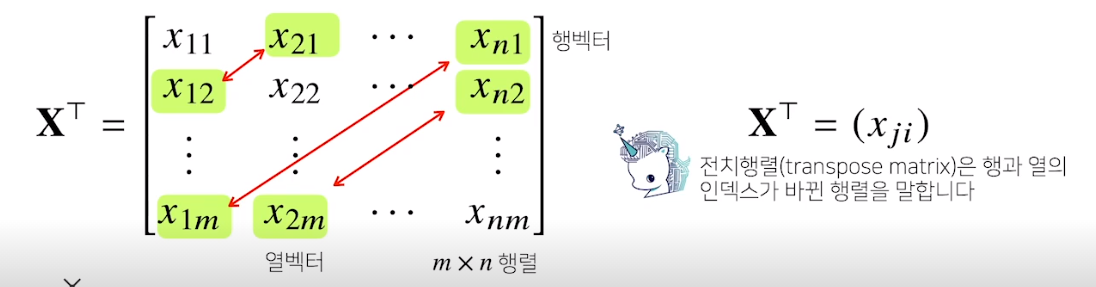
행렬의 이해

벡터가 공간에서 한점을 의미한다면 행렬은 여러점들을 나타낸다

행렬의 행벡터 xi 는 i번째 data를 의미한다

xij는 x번째 data의 j 번째 변수를 의미

행렬의 곱셈

i번째 행벡터와 j 번째 열벡터의 내적을 성분으로 가지는 행렬을 계산한다

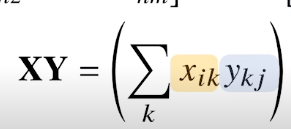
numpy에서는 @ 연산을 활용한다

행렬도 내적이 있을까

넘파이의 np.inner은 i번째 행벡터와 j째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산

수학에서 말하는 내적과 는 다른개념이다

행렬의 내적은 보통 두 행렬사이의 trace를 계산하게 되는데

numpy는 다르다

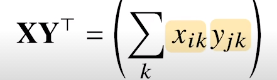
이렇게 transpose와의 행렬곱셈이 numpy에서의 innerproduct이다

행렬의 이해 2

행렬은 벡터공간에서 사용되는 연산자(operator)로 이해한다

서로다른 data를 연결시키는 연산자

m차원 공간의 점인 x와 , n차원 공간의 점인 z를 연결해줄때

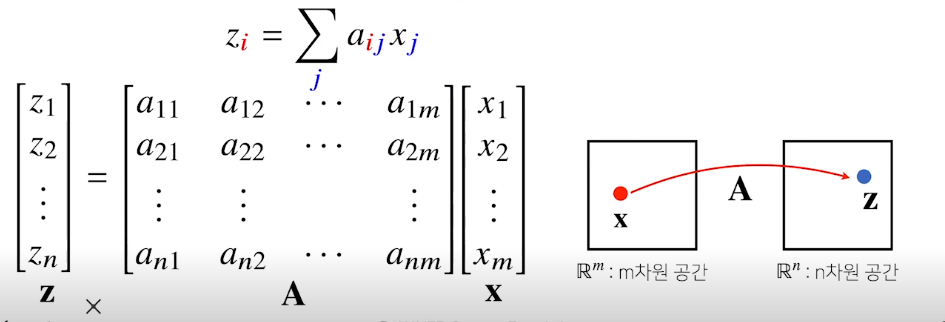
x라는 벡터에 A라는 행렬과 곱해주게 되면 새로운 Z라는 열벡터가 나온다

mapping하는 연산자!!

주어진 data에서 pattern을 추출하거나 data압축이 가능하다!!!!!

행렬을 사용하는 연산자 -> Linear Transform(선형변환)

역행렬

행과 열의 숫자가 같고 det가 0이 아니여야 한다

np.linalg.inv(x) 를 사용하여

주어진 행렬의 행의 갯수가 열의 숫자보다 많다면 ->

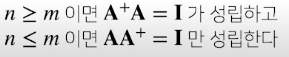
주어진 행렬의 열의 갯수가 행의 갯수보다 많다면 ->

유사역행렬을 사용하여 해중 1개를 계산

선형회귀 분석 (Linear regression)

만약 변수의 갯수보다 식의 갯수가 많은경우 -> 선형회귀로 푼다

유사역행렬을 구해서 선형회귀 방정식을 구한다

여러개의 점을 행렬로 표현후 계수벡터인 β를 곱해주게 되면 하나의 선으로 표현된다

어떠한 β를 쓸까를 구하는 -> 선형회귀 분석

미지수가 더 많기 때문에 해를 찾는것은 불가능

따라서 최대한 가까운 선을 찾는다 -> L2 norm을 사용하여

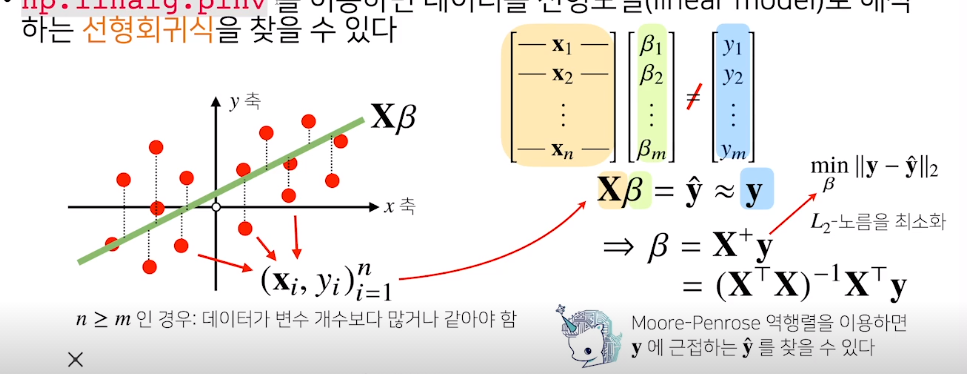
이 계수를 구하기 위해서는

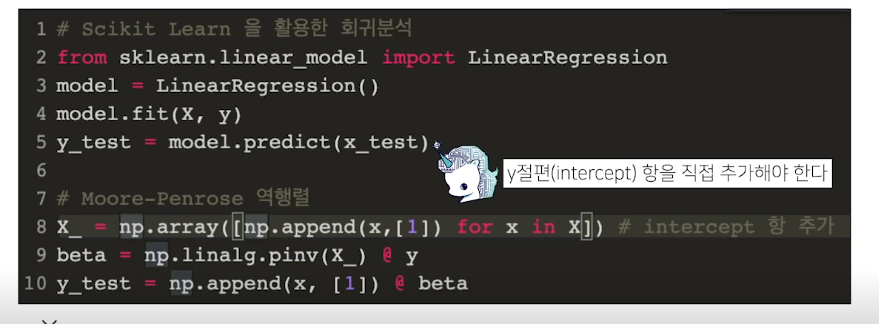
2가지의 방법이 있다. 이때 Moore-Penrose로 구하려면 y절편값을 추가해주어야 한다.

공부를 마치고 궁금한게 너무 많았다

특히 선형대수학 파트에서 이다

무어펜로즈 역행렬을 이용하여 해를 하나 구하는 과정에서

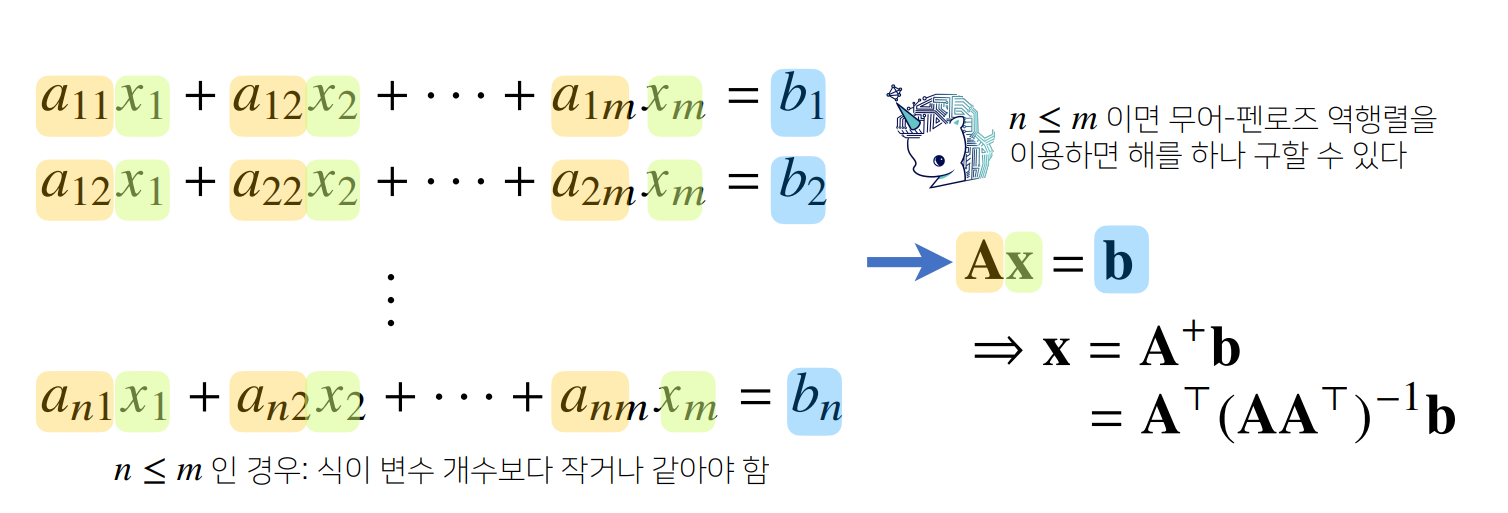
이렇게 나와있는데

A가 R^n*m^ 인 차원에서 n은 식의 갯수 m은 미지수의 갯수

m이 n보다 크기 때문에 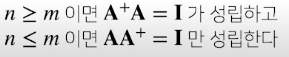이 조건을 보면 왼쪽에 곱해주어야 항등행렬이 된다

근데 AxA+가 x가 될수있나?

x가 벡터라 자리를 바꿔 곱해도 되는건가

무어 펜로즈를 다시한번 자세히 보면 조건이 생성되는 이유는

n과 m이 다를때 AA^T^ 와 A^T^A 중 하나는 역행렬이 존재하지 않는다

이 조건이 바로 m<n이면 AA^T^ 의 역행렬이 존재하지 않고, m>n이면 A^T^A의 역행렬이 존재하지 않는다

따라서 유사역행렬이 조건에 따라 저렇게 표현되는건 알겠는데

A+A나 AA+ 를 해주었을때 차원이 다르게 나올뿐이지 이게 진짜 I 가 하나는 안나오나? 컴퓨터로 돌려봐야겠다

그리고 뒤에 linear regression 부분도 너무 간단하게 알려주셔서 중요한 파트인데 더 따로 알아봐야겠다.