확률론1
Day9 : 확률론 맛보기
확률론
- 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있다.
- 손실함수의 작동원리가 데이터 공간을 확률, 통계적으로 해석
- 회귀분석에서 Loss function : L2 norm 예측오차의 분산을 최소화
- Classification에서 Loss function : CrossEntropyLoss : 모델예측의 불확실성을 최소화 하는 방향
이들의 Loss를 최소화 하기위해서는 측정하는법을 알아야함 : 이게 바로 확률론
확률분포는 데이터의 초상화
- 데이터공간을 x*y라 표기하고 D는 이 데이터 공간에서 데이터를 추출하는 분포입니다
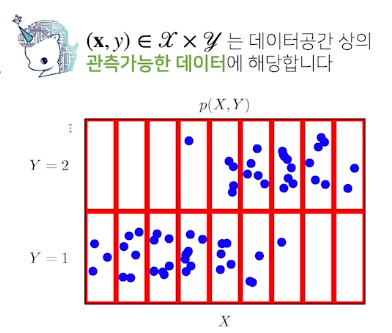
이산확률변수 vs 연속확률변수
확률변수는 확률분포 D에 따라 이산형(discrete)와 연속형 (continous)확률변수로 구분하게 됩니다
데이터 공간이 아니라 확률변수의 종류에 초점
이산형 확률변수
확률변수가 가질수있는 모든 경우의수를 모두 고려하여 확률을 모두 더해서 모델링한다
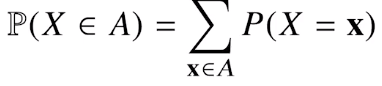
연속형 확률변수
연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density)위에서의 적분을 통해 모델링한다
확률 분포에 따라 모델링 방법에 차이가있다
그래서 접근법이 달라야 한다
data를 기반으로 모델링 할때 전체 data X,Y 분포에서
P(x,y) -> joint distribution
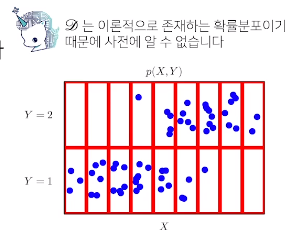
각각의 빨간 칸들에 대해서 파란점들을 COUNT한다
전체를 보면 연속확률변수 같지만 나누어 주면 이산확률분포로 생각할수 있게됨
확률 분포 D는 모르기 때문에 주어진 data의 결합분포로 원래 확률분포 D를 modeling 할 수 있다.
원래 확률분포의 D에 따라 P(x,y)의 분포가 결정되는게 아니라!!!!
원래 확률분포에 상관없이 결합분포는 무엇이든 될 수 있다.
이건 즉 modeling 방식에 따라 결정이 되는 것이다
이렇게 하는이유는
원래의 확률분포와 다르더라도 컴퓨터는 이에 근사를 시킬 수 있기때문에
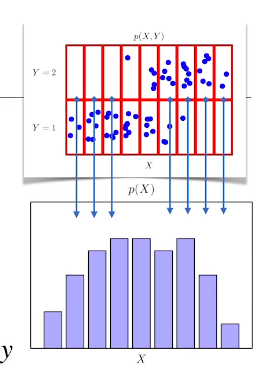
P(x)는 입력 x에 대한 주변확률분포로 y에 대한 정보를 주지는 않는다
x에 대해서 덧셈이나 적분하면 y에대한 주변확률분포를 구할 수 있다.
지금다루는 확률분포에 관한 이야기는 작년 1학기에 들었던 확률변수론에서 자세하게 다루었다
물론 focus가 전전은 조금 다르지만 학문의 기초적인 base는 비슷하기 때문에 한번 봐야겠다
조건분 y = 1일때만 counting 해주어 각각의 x값에 대한 확률분포
이게 바로 조건부 확률분포
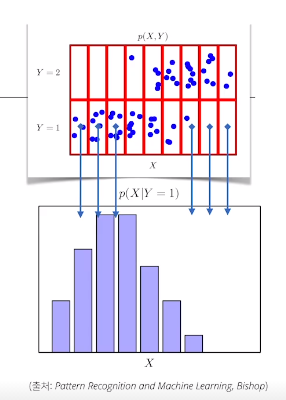
이건 입력x에 대한 y의 관계를 나타낼 수 있다.
조건부확률과 기계학습
조건부 화률 P(y|x)는 입력변수 x에 대한 정답이 y일 확률
연속 확률분포일때는 확률이 아니라 밀도임
logistic regression에서 사용했던 선형모델과 softmax의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석
분류문제에서 softmax(W$\phi$ + b)는 데이터 x로부터 추출된 특징패턴 $\phi$ (x)와 가중치 W를 통해 조건부 확률 P(y|x)를 계산한다 회귀문제의 경우 밀도함수라 조건부기대값 E[y|x]를 추정합니다
조건부 확률밀도 함수에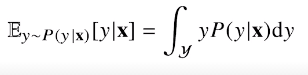 
연속이라 적분 이산확률분포면 sum의 형태로
조건부 기댓값은 L2-norm을 최소화 하는 함수와 일치한다!!!! -> 이건 이미 증명이 되어있는것 (증명과정이 필요할까?)
예측의 오차의 분산을 최소화하는 -> 조건부 기댓값
항상은 아니지만 사용함
Expectation
데이터를 대표하는 통계량
다른 통계적 함수를 사용하는데 이용하는 기댓값
학교에서 배웠던 수식과 여기서의 수식을 비교해보자
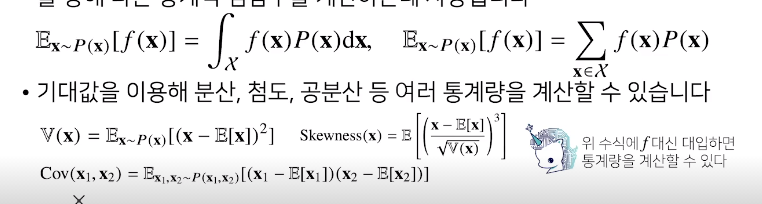
연속확률변수 : 밀도함수
이산확률 : 질량함수
딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴을 추출합니다
이특징 패턴을 학습하기 위해 어떤 손실함수를 사용할지는 기계학습의 문제와 모델에 의해 결정된다
Montecarlo Sampling
이건 강화학습에서 매우 많이 써보았다
확률분포를 명시적으로 모를때에는 데이터를 이용하여 기대값을 계산
몬테카를로 샘플링 방법을 사용해야한다
몬테카를로 예제
구간의 길이가 2이므로 적분값을 2로나누면 결국 기댓값을 계산하는것이므로 몬테카를로 사용
문제는 샘플사이즈가 많아야 오차범위가 줄어든다