Week2
week2 간단 정리 가보자 가보자~
선형회귀분석
여기서 중요한건 데이터들을 하나의 직선으로 근사하는것이다
정답 직선 -> y
데이터들의 - > x
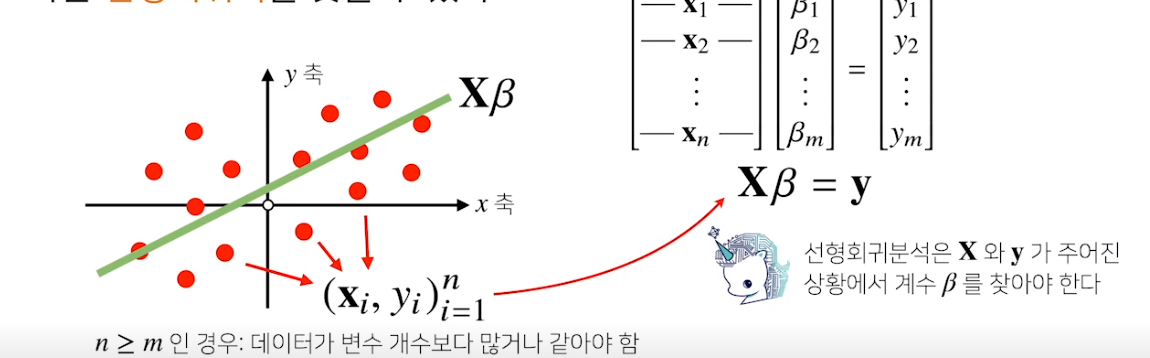
결국 이거거등 x를 y에 근사시키는거
베타를 구하는게 선형회귀분석이지
만약 n>=m 이건 결국 행이더 크다 -> 식의 갯수가 변수의 갯수보다 많다
이럼 연방 푸는게 불가능 하지 따라서 y에 근접하는 y’을 찾는거다
따라서 !!!!!
정답 y와 y’의 차이가최소화 되게 -> L2 norm을 이용해서 L2 norm을 최소화하는 B를 찾는것
이때 무어 펜로즈 역행렬 사용 해서 B를 구한다
하하하
이선형 회귀분석이랑 경사하강법이랑 무슨상관???????
무어펜로즈 사용하기 시러서 경사하강법 쓰는거지요
왜 시를까?
Reason : 지금은 선형만 하고있어서 무어랑 경사랑 상관없는데
이제 많은 실제 모델들은 비선형이다. 따라서 비선형에서도 사용 할 수 있는 경사하강법을 사용하는것!!!!!!!!
경사하강법
결국 가장중요한건 gradient vector이다
변수가 vector인 다변수 함수의 경우 편미분을 사용하여 진행
gradient
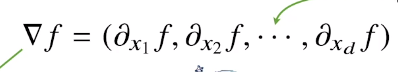
여기서 norm은 절대값을 대체하는 것
eps : 종료조건
왜냐? 완전이 grad가 0이되는건 컴이라 불가능함
var = init
grad = gradient(var)
while (norm(grad)>eps):
var = var-lr*grad
grad = gradient(var)
이제좀 gradient descent의 큰그림이 보인다
결국은 어느방향으로 움직여야 함수값이 증가하는지 감소하는지를 알려주는게 gradient로
gradient를 계속해서 update하여 norm이 0에 가까운 값이면 이제 최솟값을 보장해주는 이런 느낌적인 느낌 ㅇㅋ
근데 이제 문제는 이를 행렬을 이용한 수식으로 증명하고 전개하는것이다
요게 이제 어려운 Point 이건 손으로 작성하겠다.
Further Question
강의영상 03:47부터 소개되는 내용인, d-차원 벡터(베타)에 대한 그레디언트 벡터를 구하는 계산을 각자 직접 손으로 해보기 바랍니다!
그럼
이것도 손으로 계산해서 update (with ipad)
딥러닝 학습방법 이해하기
딥러닝은 비선형 모델을 해석하는 것이다
그 전에 먼저 선형모델을 다루어 보자
신경망을 수식으로 분해

이게 가장 중요한 수식
다시 행렬 review를 해보면 X는 데이터들의 집합 xi는 i번째 data xij는 i번쨰 data의 j번째 변수값
다시말해 nxd 인 X행렬은 n개의 data를 가지고 각데이터는 d개의 변수를가짐.
W는 data를 다른 차원에 mapping해주는 역할을 한다. 데이터에 가중치를 곱하고 bias를 더해주는 이런느낌
Softmax
- 분류문제를 풀때 선형모델의 출력과 softmax의 결합으로 특정벡터가 어느 클래스에 속하는지 알 수 있음
- 벡터를 확률로 변환하는 함수이다
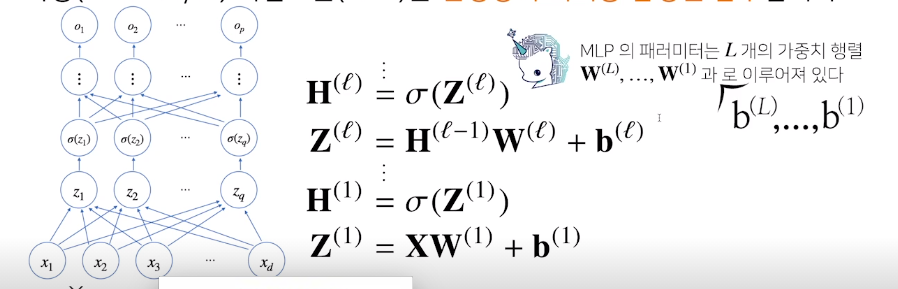
위와 같이 순차적으로 가중치와 bias를 계산한 값을 다음노드에 또 집어넣고 계속해서 순방향으로 전파 -> forward propagation
학습할때는 back propagation을 사용
Back Propagation
선형회귀분석에서 B에 해당하는 gradient벡터를 계산해서 업데이트 했던것처럼 각층에 존재하는 parameter의 미분값을 계산해서 업데이트
각층의 가중치에 대한 gradient벡터를 계산하는 법
행렬들의 원소의 모든 개수만큼 경사하강법이 적용이 된다
한층일때는 목적식에 대한 gradient 벡터를 동시에 계산할 수 있지만, 딥러닝의 경우 gradient 벡터를 순차적(back propagation)으로 계산하게된다
손실함수 –> L일떄 우측을 계산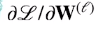
위층에 있는 gradient를 계산한 다음에 chain rule을 이용해 아래층의 gradient를 계산

이러하게 계속해서 각 가중치에 대한 gradient vector를 구한뒤 이들을 SGD를 사용해서 Loss function을 update시킨다
확률론 맛보기
- 회귀분석에서 손실함수로 사용되는 L2 norm은 예측오차의 분산을 최소화하는 방향으로 학습하도록 유도
- Cross-Entropy는 모델예측의 불확실성을 최소화 하는 방향으로 학습하도록 유도
- 분산 및 불확실성을 최소화 하는 방법을 알아야 함
이산확률변수 VS 연속확률변수
위의 개념이 결국은 가장 중요하다
이산은 경우의수를 다 고려해서 확률을 구함
연속은 밀도함수를 적분해서 확률을 구함