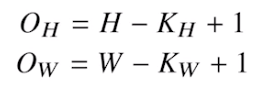CNN1
CNN
Convolution 연산 이해하기
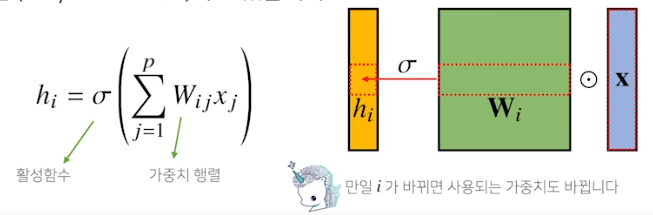
지금까지 배운 MLP는 fully connected. 가중치 행들이 i번째 위치마다 필요해서 i가 커지면 가중치 행렬의 크기가 커지게 됨
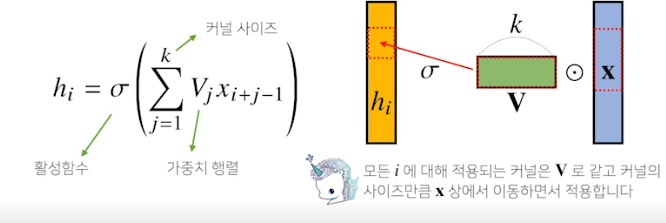
우리가 이제부터 볼 Convolution 연산은 커널이라는 고정된 가중치 행렬을 사용하여 고정된 커널을 입력벡터에서 옮겨가며 적용
x라는 입력벡터 상에서 커널사이즈 만큼 움직여 가며 연산
다양한 차원에서의 Convolution
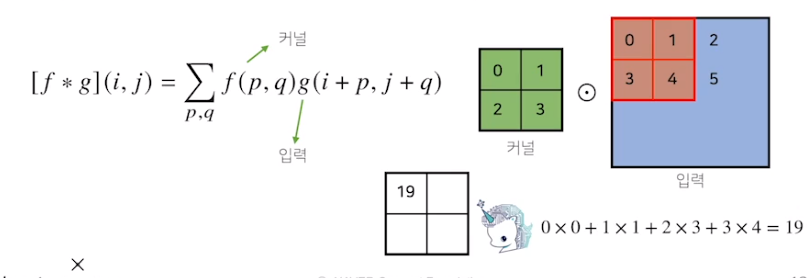
2차원 Convolution 연산
입력을 kernal size에 맞춰서 입력위치에 해당하는 index만큼 옮겨다니면서, 성분곱을 연산하는
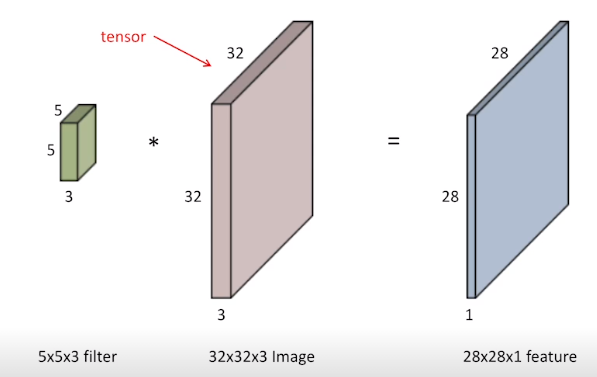
2D 이미지 다른 kernel을 적용하여 Convolution filter를 적용하면 kernel에 맞는 특성을 가지는 2D 이미지가 나온다
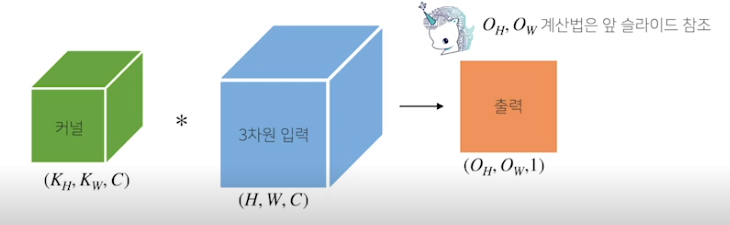
입력크기를 (H,W), 커널크기를 (K
H, KW), 출력크기를 (OH, OW)라 할때
- channel이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다 (2차원 이미지더라도, RGB가있어서 3 channel)
- 채널이 여러개인 입력인 경우 커널도 채널의 개수만큼 있어야 한다
- 채널이 여러개일때는 각커널을 적용한 각각의 채널의 결과를 더해준다
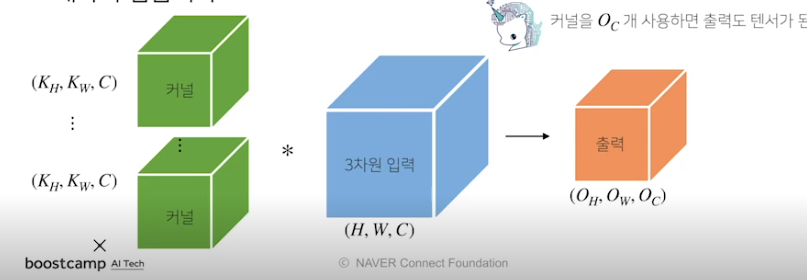
만약 출력의 channel을 늘리고 싶다면???
커널의 개수를 여러개 만들면 된다.
feature map의 채널 숫자를 늘리는 보통 이렇게 많이 사용한다
Convolution 연산의 Backpropagation
- Convolution연산은 모든 입력데이터에 공통으로 커널이 적용되기 때문에 역전파 계산시에도 convolution이 나오게 된다
Stack of Convolution
MLP때와 마찬가지로 non-linear activation을 사이에 적용했다
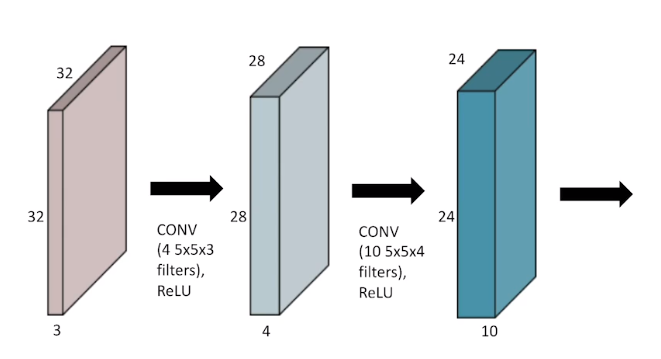
연산을 정의하는 Parameter의 숫자가 중요
첫번째 Convolutional filter의 parameter수 : 5*5*3*4 = 300 개
두번째 Convolutional filter의 parameter수 : 5*5*4*10 = 1000개
Convolution NN
- CNN은 Convolution layer + Pooling layer + fully connected layer
- Convolution & pooling layer : feature extraction
- fully connected layer : decision making
점점 뒤의 fully connected layer를 줄이는 추세
reason : parameter의 수
우리가 일반적으로 우리의 모델의 parameter 숫자가 늘어날수록 학습이 어렵고 generalize performace가 떨어진다
따라서 CNN은 parameter수를 줄이는데 집중한다
어떤 뉴럴네트워크에 대해서 parameter숫자를 계산해보자
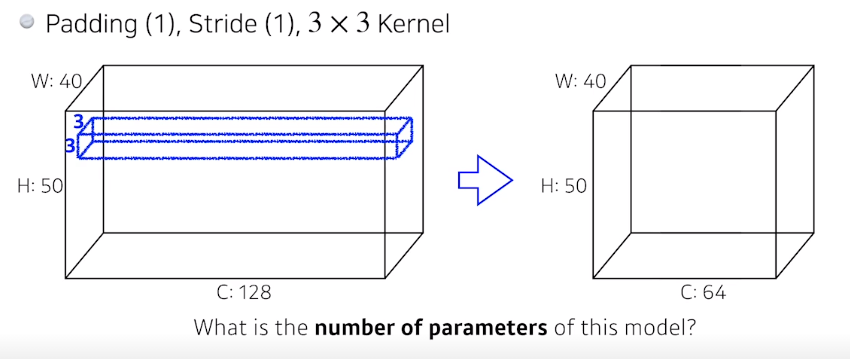
Stride & Padding
skip
Convolution Arithmatic
우리가 사용하는 kernel을 계산해보면
일단 3*3의 width 와 height이며 kernel의 channel은 입력의 channel과 같아야 하므로 128이다
따라서 하나의 kernel의 size = 3*3*128이다
이제 이 kernel의 갯수를 찾으려면 output의 channel인 64이다
따라서 총 parameter의 개수는 3*3*128*64 = 73728이다
이제 padding과 stride는 parameter 수와는 연관이 없다
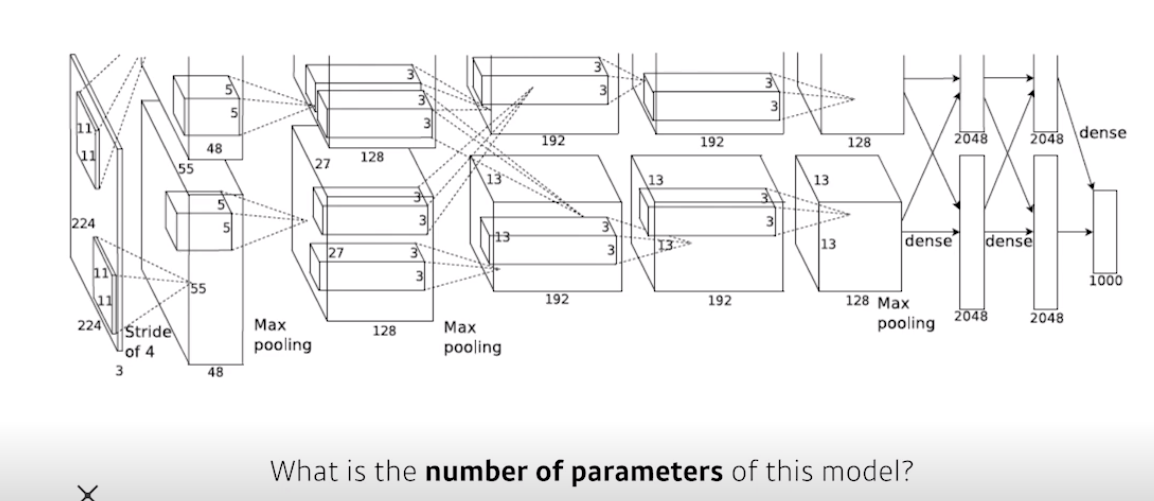
사실 alexnet은 network가 2 path로 나누어짐
일단 첫번째 layer의 kernel = 11x11x3 = 363
이게 48개 있으므로 parameter개수 = 17424개
원래는 이제 96짜리 channel을 만들었어야 되는데 2개로 나누어서 48 channel로 만들어줌
따라서 총 parameter수 = 34848
kernel = 5x5x48 = 1200
이게 128개 그리고 총 2개 있으니 -> 1200x128x2 = 307k
kernel = 3x3x128 = 1152 이게 2개 -> 2304
이게 192개 그리고 총 -> 2304x192x2 = 884k
똑같은 방법 -> 663k
쭉쭉
그러다가 Fully connected layer의 parameter 개수
13x13x128x2x2048x2 = 177M
16M
4M
보면 dense layer에서 parameter숫자가 너무 커진다
결국은 parameter를 줄이기 위해서는 convolution layer를 깊게 쌓고 뒤의 dense layer를 최대한 줄이는 방향으로 발전하고 있다
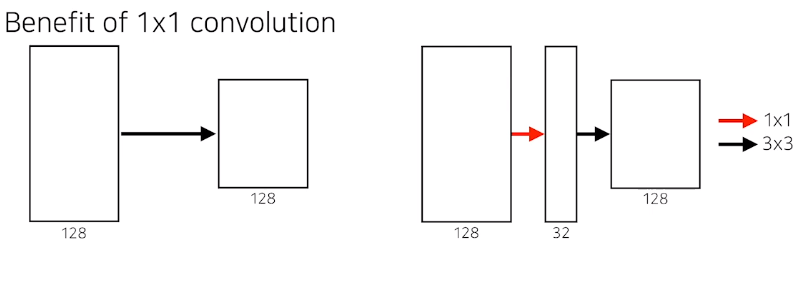
1x1 convolution
여기서 parameter수를 계산해보면 1x1x128x32 = 4096
demension을 줄인다!!!
깊이는 깊어지지만 parameter수를 줄이는 역할을 한다
e.g) bottle neck architecture
Modern Convolutional Neural Networks
ILSVRC에서 우승하거나 좋은 성능을 거둔 model들에 대한 parameter 개수, depth 등등
AlexNet
ILSVRC
Imagenet Large-Scale Visual Recognition Challenge
1000 different categories
over 1 millions images
AlexNet
- gpu의 성능이 부족해서 한번에 계산이 안되서 2개로 나눠서 따로 training을 시킴
Receptive field : 하나의 kernel이 볼수있는 이미지 level에서의 영역은 커짐, 그러나 parameter가 늘어나게 됨
- 5 Convolutional layer
- 3 Dense layer
Key idea
use ReLU function (non-linear func, 마지막 slope가 1이라 gradient가 사라지거나 네트워크를 망칠 확률이 적음)
preserve properties of linear model
overcome the gradient vanishing problem
이전에 많이 활용하던 tanh나 sigmoid는 값이 크면 output의 gradient가 0에 가깝게 나온다
GPI implementation (2 GPU)
Overlapping Pooling, Local response normalization
Data augmentation
Dropout
지금 보면 별로 대단한게 아니지만, 그당시에는 혁신적인 방법
일반적인 standard 를 잡았다!
VGGNet
Increasing depth with 3x3 convolution filter
1x1 convolution filter
Dropout (p=0.5)
VFF16,VGG19
Why 3x3????
kernel size가 커지면서 가지는 이점 : Receptive field가 커진다
ex)
3x3을 2번 하게 되면 output의 1개의 값은 input의 5x5를 보게된다 -> 이게 바로 Receptive field
3x3을 3번 하게 되면 output의 1개의 값은 input의 6x6을 보게된다
따라서 3x3을 2개 사용하는 것과, 5x5를 1개 사용하는 것은 receptive field의 관점에서는 같다
따라서 이둘의 parameter의 개수를 비교해 보면 (chaneel : 128)
3x3 2개 : 3x3x128x128x2 = 294k
5x5 1개 : 5x5x128x128 = 409k
따라서 3x3 2개를 쓰는게 parameter의 숫자 감소 측면에서 이득이다
왜이런일이 일어날까?
사실상 3x3x3 = 27, 6x6 = 36 | 3x3 = 9, 5x5 = 25 이런 맥락이다
뒤의 대부분을보면 kernel은 7x7을 벗어나지 않는다
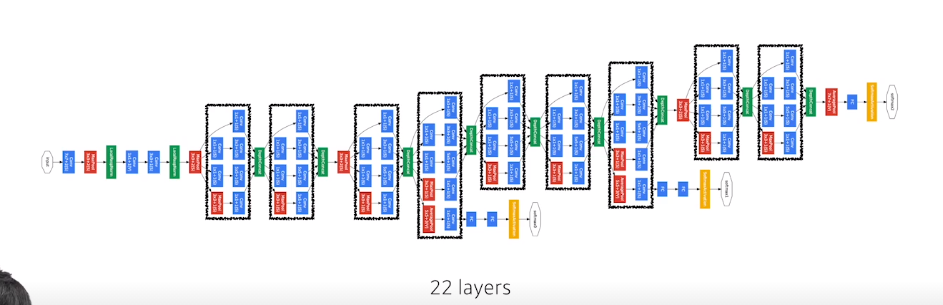
GoogLeNet
보면 전체 network 안에 작은 network 구조들이 반복되고 있다 (network in network)
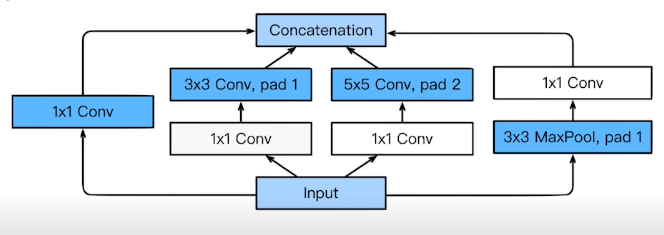
- Inception block 활용
하나의 입력에 대해서 여러개의 receptive field를 가지는 filter를 거치고 이들을 concatenation
하지만 그보다 중요한게 중간중간에 추가로 들어간 1x1 Conv
- 3x3x128x128 = 147456
- 1x1x128x32 = 4096, 3x3x32x128 = 36864 ->합은 : 40960
parameter 수가 1/4로 줄었다 —-> 사용하는게 이득이다!!!
과연 AlexNet,VGGNet, GoogLeNet 중 parameter수가 작은것은?
- AlexNet(8 layer) : 60M
- VGGNet(19-layer) : 110M
- GoogLeNet(22 layer) : 4M
ResNet
- Deeper neural networks are hard to train
- Overfitting is usually caused by an excessive number of parameters
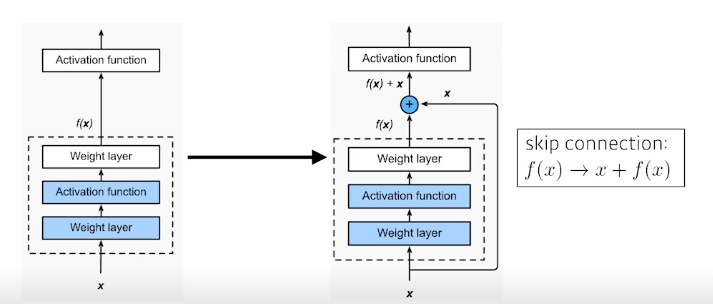
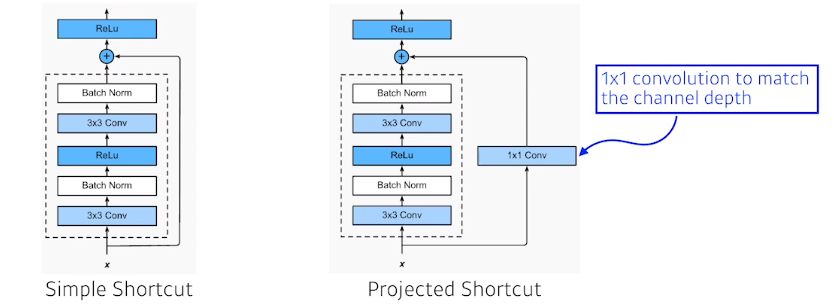
Identity map
x와 output의 차원을 맞춰주기 위해서 1x1 convolution으로 사용하는것
- Convolution 연산과 batch norm의 순서??????
- 더 자세한 ResNet의 구조????
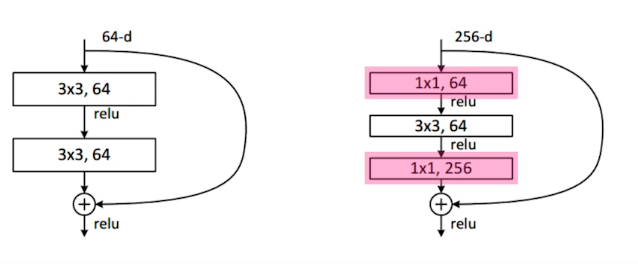
Bottleneck architecture
3x3의 연산을 하기 전에 channel 수를 줄이게 되면 parameter의 숫자를 줄일수 있지 않을까?
DenseNet
- ResNet을 바라보게 되면 그냥 두개의 값을 더하지 말고 concatnate시키면 되지 않을까?
- 계속 concatnate하면 channel이 기하급수적으로 커지기 때문에 이를 해결하기 위해 중간에 1x1 conv를 해줌