딥러닝 기초
베이즈 통계학
- 데이터가 추가되었을때 쓰는 인과관계에 대한 추론법
조건부 확률
- 베이즈 정리는 곧 조건부 확률을 이용하여 정보를 갱신하는 방법을 알려줍니다
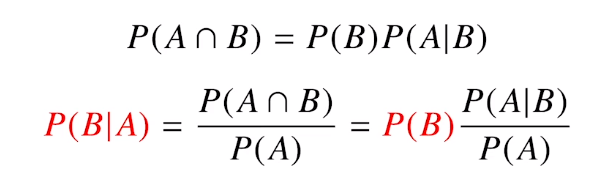
결국 우리가 알고 싶은 것은 A라는 새로운 추가적인 정보가 들어왔을때 P(B)로 부터 P(B l A)를 계산하는 방법을 제공한다
실제로 그럼 어디에 쓸까

- D : data , $\theta$ : 모수
- 사후확률 : 데이터가 주어져 있을때 $\theta$에 대한 확률
- 사전확률 : 데이터가 없는 상황에서 사전에 주어진 $\theta$ 에 대한 확률
- Likelihood : 현재 주어진 모수에서 어떠한 Data가 관찰될 확률
- Evidence : Data 자체의 분포
ex) COVID의 발병률이 10%로 알려져 있을 때, 이 바이러스에 실제로 걸렸을때(조건부) 검진될 확률 : 99%, 오검진 확률 : 1%
이 때, 어떤 사람이 양성판정일때 정말로 이사람이 바이러스에 감였되었을 확률
발병률 : 사전확률
실제로 걸렸을 확률 : $\theta$
검진된 경우 : D
실제로 걸렸을 때 검진될 확률 : P(D l $\theta$) : Likelihood
가능도와 사전확률이 주어져 있으므로, 사후확률 계산가능
그렇다면 Evidence의 계산법은????????
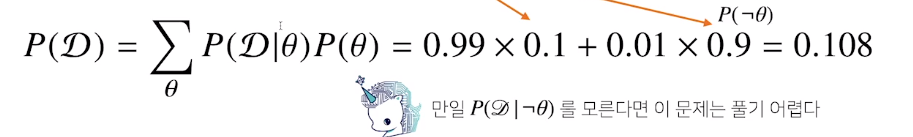
따라서 $\theta$를 부정했을때의 likelihood도 알아야 계산이 가능하다
조건부 확률의 시각화
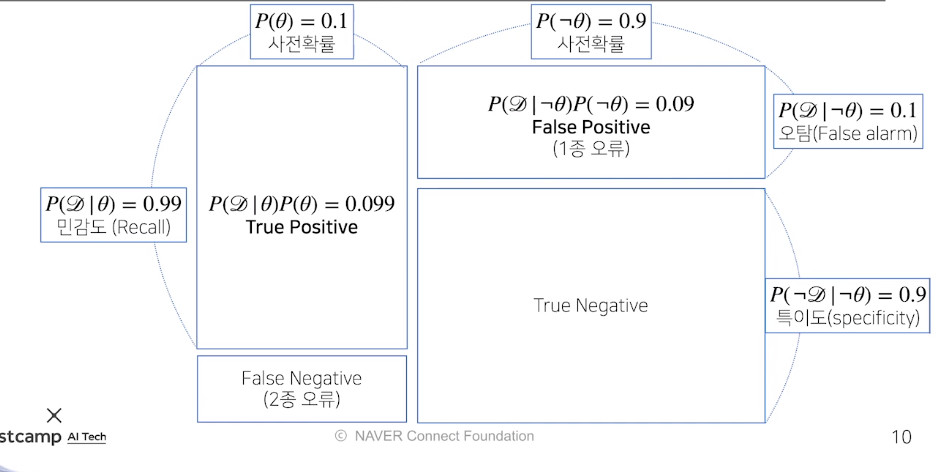
데이터의 성격에 따라 1종오류을 줄이냐 2종오류를 줄이냐가 달라진다
Ex) 의료문제의 경우 False Negative : 질병이 아니다라고 했는데 실제로 질병일 경우 따라서 False Negative에 신경을 쓴다
사전 확률 : 질병에 걸릴 확률, 안걸릴 확률
민감도 : 걸린걸 걸렸다고 탐지
실제로 걸렸을 때 걸렸다고 할 확률 : 민감도
실제로 걸리지 않았을때 걸렸다고 할 확률 : 오탐
양성이 나왔을때 진짜 양성인 경우 : True Positive
음성이 나왔을때 진짜 음성인 경우 : True Negative
양성이 나왔을때 음성인 경우 : 1종 오류
음성이 나왔는데 질병에 걸린 경우 : 2종 오류
정밀도 : TP/(TP+FP)
베이즈 정리를 통한 정보의 갱신
- 베이즈 정리를 통해 새로운 데이터가 들어왔을 경우 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산가능
- 앞서 양성 판정을 받은 사람이 2번째 검진을 받았을 때도 양성이 나왔을때 진짜 COVID에 걸렸을 확률은?>??????
베이즈 정리를 활용하여 사후확률을 연속으로 계산해보면 정밀도가 화아아악 올라간다
이게 바로 베이즈 정리의 강점!!
- BUT!!! 조건부확률로 인과관계를 추론해서는 안된다!!!!!!!!!!!
- 인과 관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 고려해 주어야 한다
- 인과 관계를 고려했을 시에 예측도는 떨어질 수 있음
- 인과 관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다
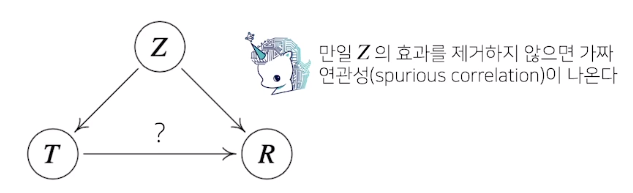
ex) 키와 지능 -> 여기에 나이에 따른 효과를 제거하지 않는다면 키가 클수록 지능이 높다라는 결과가 나오게 됨
이러한 나이와 같은 중첩요인을 제거하는 것이 Main Point
Ex)
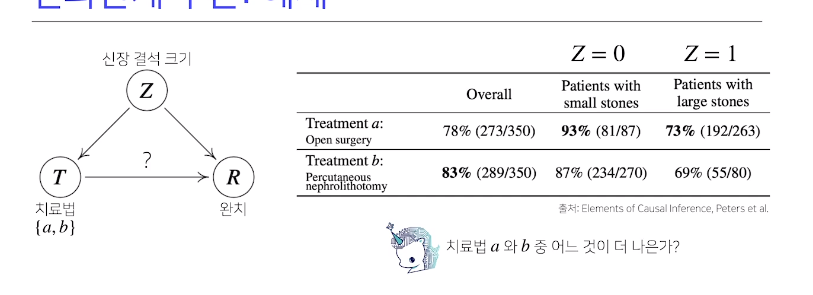
위의 문제가 바로 아주 유명한 simpsons 역설
a와b의 중첩효과를 제거해야 됨
Z의 개입을 제거하기 위해 조정(intervention)효과를 사용한다???
조정효과에 대한 개념이 조금 필요할듯 싶다
Deep Learning ; Historical Review
사람의 지능을 모방하는 인공지능 AI > data based Machine Learning > Deep Learning (NN을 사용하는)
Key components of Deep learning
- Data that model can learn
- Model how to transform data
- Loss Function that quantifies the badness of model
- Algorithm to adjust the parameters to minimize the Loss Function (최적화 알고리즘)
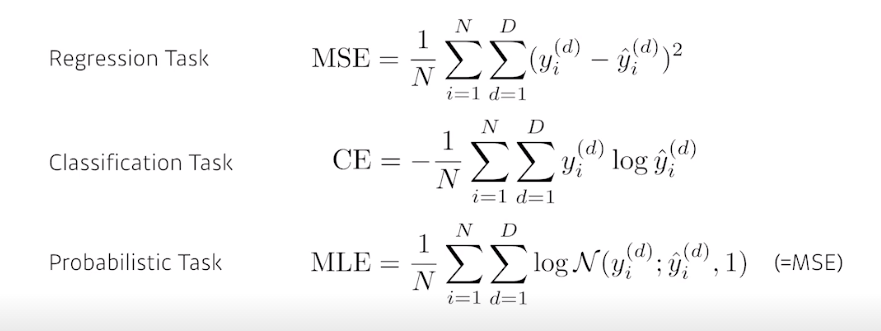
Historical Review
1. AlexNet
- 224*224의 image data 분류대회에서 처음으로 Deep Learning을 사용하여 1등함
- 실제적으로 딥러닝의 성능이 입증이 되었던 사실
2. DQN
- Q -Learning의 function estimation에 NN을 추가하여 높은 성능을 이끌어냄
3. Encoder/Decoder
- NLP의 trend가 많이 바뀌었다
4. Adam Optimizer
- 우리가 optimizer를 선정할때 Adam을 그냥 쓰는 이유가 있을까? 결과가 잘나오는 이유가 있을까?
5. GAN
- Generate Model : Network가 data를 생성!
6. RESNET
- 왜 딥러닝이냐를 설명해주었다
- Layer를 더욱더 깊게 쌓을수 있게 만들어줌
7. Transformer
- Attention is all you need!!
- 모든 기존의 RNN을 대체하였고, 이젠 CNN도 넘보고 있다
8. BERT (fine tuned NLP model)
- 일반적인 단어들로 model을 train한후에 내가 원하는 소수의 data에 fine tunning
- OPENAI의 GPT-3
9. Self Supervised Learning
- 이미지 분류와 같은 분류문제를 풀때 한정된 학습데이터로 model과 loss fun을 바꿔가는게 아닌 학습데이터 외에 라벨을 모르는 Unsupervised Learning 활용
- SimCLR
Neural Networks
단순히 Function approximate이다
gradient ascent 라면 reward를 키우도록 ! 이런게 되겠구만
step size $\eta$
행렬을 찾겠다 -> 서로다른 차원의 선형변환을 찾겠다
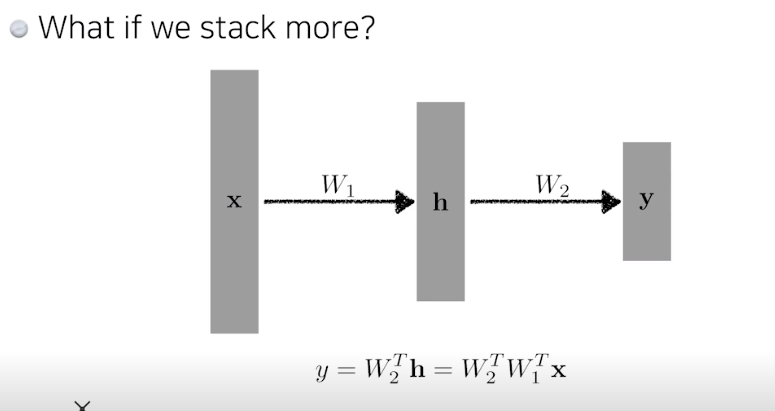
이렇게 그저 연속된 선형변환은 하나의 선형변환으로 합쳐질수 있기 떄문에 층을 여러개 쌓는 이유가 사라진다
따라서 층 중간에 activation function을 넣어준다 -> nonlinear transform
선형결합의 반복이 아닌 nonlinear transform의 결합
더 많은 표현력을 가지게 됨
존재성이 중요한게 아니라 표현력이 중요함
MSE는 제곱이라 data 사이에 error가 껴있을때 -> 전체적인 NN이 망가질수도 있음
이렇게 항상 같은 Loss Function을 쓰는게 아니라 상황에 맞게
다른 값에 비해서 그값이 높기만 하면 그 index를 뽑는것 -> 그래서 이걸 수학적으로 CE를 사용함